Tree Programming
BigObject allows users to apply their functions in FIND statement. Concept wise, BigObject will first construct a tree object based on the FIND description, apply user's function, and then place those nodes evaluated to TRUE in the result table. The whole process is illustrated as in the following figure.
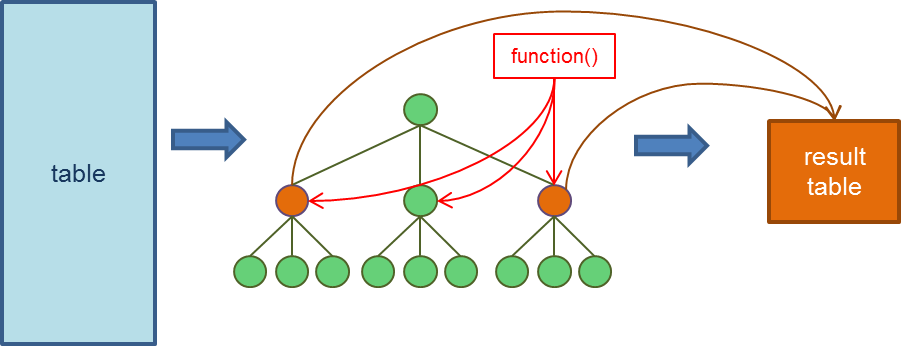
As an example, following FIND statement can be used to find the number of distinct customers for each product brand:
FIND dcount() Product.brand IN Customer.id FROM salesHow the statement works is depicted below. A hierarchical tree object is created such that all transactions which belong to the same brand, and then to the same customers are grouped together. Function dcount() is evaluated for each node at the Product.brand level. Finally, the number of distinct customers for each brand is reported in the result table.
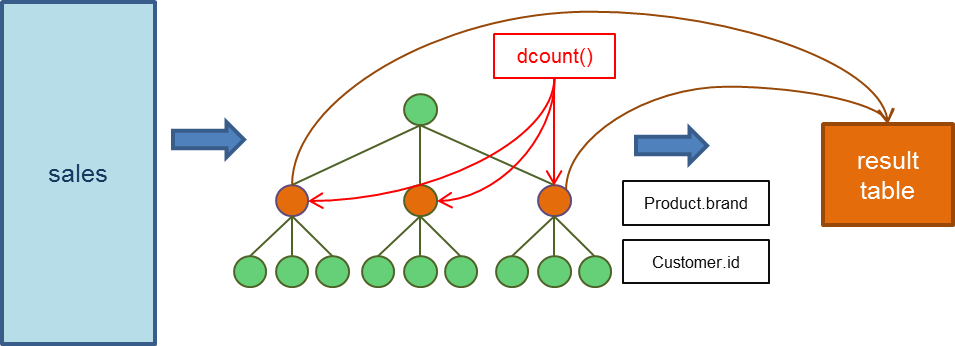
The fucntion dcount() used in the above FIND statement is as follows:
function dcount(n)
dc = n:count()
n:setValue(0 , dc)
return true
endThe argument n denotes the tree node that is currently evaluated. Function dcount() applies the built-in function count() to obtain the number of children (i.e., this distinct number of customers). And then it uses assign() function to place the distinct value in the first data field (denoted as 0) of node n. Note that function dcount() always returns TRUE, which means all nodes at level Product.brand will be reported in the result table. An example result table is listed below:
| Product.brand | _VALUE |
|---|---|
| Fanta | 1186 |
| Coca-Cola | 5327 |
| Pepsi | 8397 |
| ... | ... |
The distinct number of customers for each product brand is listed in the column _VALUE. It is the first data field for each tree node and created by FIND implicitly. Its value will be included in the result table by default.
The root of sub-tree that is currently being evaluated is always specified as the first argument.
Now assume that a user only wants to report those product brands having more distinct customers than a threshold. We can modify the above dcount() function as follows:
function dcount(n, ts)
dc = n:count()
tr = tonumber(ts)
n:setValue(0 , dc)
if (dc > tr) then
return true
else
return false
end
endThe threshold value is passed via argument ts. It can be easily seen that only those nodes with more children than the threshold will return TRUE. Note that all arguments besides the tree node n are passed in string type. Therefore, one has to use tonumber() to convert it into a number first.
Thus, the FIND statement to obtain all product brands with more than 1500 distinct customers is straightforward:
FIND dcount(1500) Product.brand IN Customer.id FROM salesDepth-first-traveral
Function children() returns an iterator over the children of the given node. It is easy to perform a depth-first-traversal of a given node as shown below:
function dfs(n)
for c in n:children() do
dfs(c)
end
return true
end A Concrete Example: 80-20 Rule (Pareto Principle)
This example demonstrates how to use in-place programming for FIND to implement a general function "Pareto principle (the 80–20 rule) " as seen in our find by pattern example.
Assume the following FIND statement is used:
FIND pareto(80,20) Product.brand IN Customer.gender BY SUM(total_price) FROM salesFirst, the above statement creates a tree object with a hierarchy from Product.brand to Customer.gender. Furthermore, each node includes two data fields: _VALUE and SUM(total_price). The _VALUE field is used to store the computed result. The tree creation is equal to the following CREATE TREE statement:
CREATE TREE temp(_VALUE DOUBLE, SUM(total_price)) FROM sales GROUP BY Product.brand, Customer.genderThe function "pareto()" used is listed as below:
function pareto(a, threshold, percent)
sv = a:getChildrenValue(1);
value = nBinPercent(sv, percent)
a:setValue(0, value)
if value > (threshold / 100) then
return true
end
return false
end- Line 1: The first argument a is the node to be evaluated. The second argument threshold denotes the threshold (80 in the above example). And the third argument percent denotes the percentage (20 in this case).
- Line 2 : The getChildrenValue() function is used to retrieve the date field indexed at 1 of all children, which is data field SUM(total_price).
- Line 3 : The function nBinPercent() is used to compute the accumulated percentage of the first n% bin.
- Line 4 : It assigns the result to the _VALUE field.
- Line 5 ~ 8 : It returns TRUE when the result is greater than the threshold.
Function nBinPercent() is defined as follows:
function nBinPercent(data_array, npercent)
npercent = npercent / 100
sum = 0.0
for i,v in ipairs(data_array) do
sum = sum + v
end
check_size = npercent * #data_array
table.sort(data_array, function(a,b) return a>b end)
temp_sum = 0.0
for i = 1, math.floor(check_size) do
temp_sum = temp_sum + data_array[i]
end
return temp_sum / sum
endPlease refer to our Lua on GitHub for more examples.